This is an archived version of the original blogpost from the devblog of the game Spliff Spacey by Frozen Walruss studios. As the original post seems to have vanished I decided to host a backup to preserve this knowledge.
It’s difficult to get equipment to be ‘balanced’. Games with any sort of visible variables (like equipment and stat boosts) are hard to make because they involve numbers, and numbers have a way of catching up to you. If you just haphazardly throw numbers together and don’t have a plan you run into extreme balance issues or, even worse, boring equipment upgrades.
As someone who hated math in college, I’m here to help you use some mathematical functions and to think about them in non-math ways. Think of them more as magic cheat sheets. I’ll be taking some liberties with my language to make this more accessible, so if you’re a math whiz please be gentle. I’ll stick to generic fantasy for a lot of these examples even though Spiff Spacely Saves The Universe is sci-fi, but keep in mind you could use it for increasing enemy difficulty, armor improvements, weapon damage, when to learn spells or abilities, or all sorts of things that could apply to multiple genres. Try to think of examples for your game!
To balance equipment, I have two goals.
- Make changes fit onto a predictable curve
- Make things created on that curve be applicable for in-game use
This article is going to focus on #1. The reason making equipment fit onto a predictable curve is so you can balance things ahead of time.
If you have a sword that does 10 damage and a shield that blocks 3 damage and decide you want a “level 2″ sword and shield, it’s tempting to just fudge the numbers a bit based on how they apply to the game pieces immediately around them. Your 10 damage sword might kill an initial enemy with 15 hp in two hits, so you make a level 2 sword have 15 damage so it kills it in one. Upgrade!
The problem with this is that you have no idea what a level 10 sword will be when you’re balancing around level one. This is especially true if you don’t even have the enemies balanced yet for that area. What if you also introduce axes as weapons? What about enemies that take 100 hits to kill, should they just take one less hit to kill? That’s a 1% decrease in hits required instead of the 50% decrease found with the 15 hp enemy your level 2 sword could kill in one hit. Would upgrading even be important?
It’s a nightmare, especially with iterative design.
When balancing on an obvious curve, you just pick a different point on the curve. You have your level one 10 damage sword at one point and when you say “what will a level 10 sword be”, you just move to that point on the curve. This helps you figure out what you’ll likely be dealing with in the future and, as you get more things laid out in advance, you can balance them off each other. It starts to feel like magic!
To do this we will use a variety of functions depending on what we want to accomplish. I’ve got a spreadsheet all laid out for you that you can download here:
RPG-Functions-Workbook-Download
I highly suggest following along with the article and plugging in your own numbers. For your convenience, all the results of the equations are in green and the cells you put numbers into are in orange.
Go ahead and open up the Excel workbook and open up the “Linear Equation” worksheet. You won’t get much out of this if you don’t!
Linear Function
A linear function is probably the least useful and also the easiest to understand. A linear function is what you use to make things grow at a constant rate. “Every 5 levels you learn a new ability” is an example of a linear function in action. The gap between two points on a line created by a Linear Function are the same as the gap between any other two points! You probably saw this first as y = mx+b.
We’re filling in gaps in that equation with numbers that we choose. We make that line have the angle we want to illustrate something the game will be providing us. It’ll all make sense in a moment, I promise.
To think of this in a non-mathematical way, the “Y” is the number we’ll end up using and the “X” is the variable that we change to make it work the way we want.
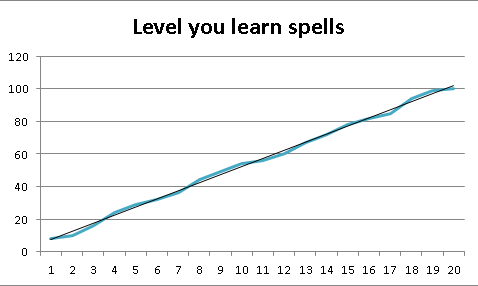
So for our example, we want the player to learn an ability or spell every so many levels. “Y” is going to show us what that level is. X is going to define why that level is.
That “M” and “B” for our formula are going to act as constants. It means they don’t change; the stuff around them does!
So the “Y”, what we’re changing with the equation, is “Level you learn spells”.
The X for us is can be anything we want, but its best to be consistent with our goals. I’ll simply make X (column E) go up by 1 for each Spell my character has already learned. I’ve chosen this because “spells learned” is a good way to track progress and is typically a simple number. I could also do something like “bosses defeated” or the like as well, but this suits my goals just fine.
Our “Y=mx+b” formula now looks like this:
Level you learn a Spell = ? * Spell Count + ?
So what do we do about those question marks? If you look at the equation, the first one is the multiplier (column D), the second one is an arbitrary constant that we just add on (column F). Let’s simplify and think about it from a game perspective. We’ll make the arbitrary addition “0” and the multiplier “1” and see what it looks like.
Level you Learn a Spell = 1(Spell Count) + 0
Our first linear function! It says “You will learn an ability every level”, assuming you start with at least one. If we wanted to make it to where we learned an ability every level multiple of 5, we’d simply change the multiplier to “5” instead of “1”. By level 100, you’ll learn 20 abilities.
Pretty boring and predictable, right? That’s when we can use the second number! By adding to the equation, it changes the result. If we changed “0” to “7” in column F, we’d get 5 * 1 + 7 = 12, and 5 * 2 + 7 = 17, etc., etc. Still boring and predictable, but a little less obvious than multiplies of 5. To REALLY make it interesting, we use a randomized number there.
By using Excel’s RANDBETWEEN() function, we can make the overall trend the same but the individual outcomes different! The greater the range, the greater the variance. I still want roughly every 5 levels to have a new spell, so I’ll keep it small: 0 through 4. You can see no matter how many times you update it, the outcome is still roughly the same.
To an outside observer that looks at the end result, it looks very meticulously designed. To us, its just slight variations in a formula. Now you have a good starting point to assign values. Go back and edit the multiplier if you decide people should earn consistently less or more, and edit the arbitrary number range if you think it should be more or less consistent. Thanks to this formula, it does everything for you whenever you want to make changes!
You can use this for all sorts of things, but the best use is a starting point. You give yourself a rough idea of what you want, like learning an ability every 5 levels or gaining 10 HP every level, then add in variance to give it some spice. Using this kind of linear equation as a starting point and editing these numbers constrains your choices and helps you think ahead.
Exponential and Polynomial Functions
Let’s say you want your game to continually get harder and you want the player to struggle to keep up with monster strength. Your game’s “thing” is exponentially increasing in difficulty.
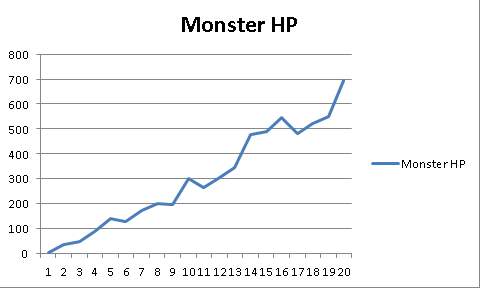
What kind of function do you use for that? Exponential functions, of course! For this example, let’s use “monster HP”. You plan for player damage to increase, so you need HP to increase with it. Open up the Exponential Function worksheet in the Excel document and follow along.
F(x) = A to the X power
Ignore the “f of x” thing. For our purposes it’s just a new way of writing Y . (Math people please don’t hurt me)
What are we trying to change? Monster HP. That’ll be the result, or the Y.
How do we change it? Well, Monster Level is a good enough way to do it. That’ll be “A” (column C).
So “Monster Level” to the “something” power. Our arbitrary value here determines how big a deal this’ll all be.
If you’re unfamiliar with exponents, 2^3 would look like this: 2 x 2 x 2. So 2^4 would look like this: 2 x 2 x 2 x 2. Whatever the exponent (the little number) is, that’s how many times the base number is multiplying itself by.
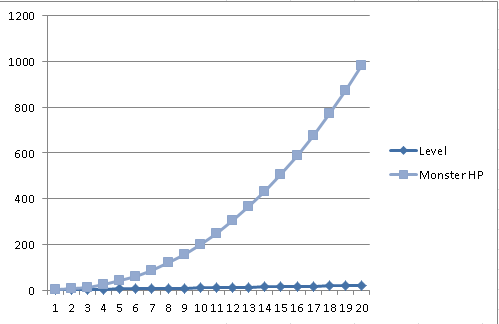
Let’s start small and say that the Monster’s HP is its level to the second power. So (Level) times (Level).
Without even using excel we can see that (level 2) times ( level2) is four, and level 3 will end up being an HP of 9. Pretty slow growth in the beginning, but level 19 is 361 and level 20 is 400. That’s a 40 point growth rather than a 5 point growth.
Let’s make it Monster Level^3 by changing column D’s cells to “3” and see where that takes us.
Level 2 is now 8 HP and level 3 is 27 HP; that’s a 19 point gap instead of a 5 point gap right off the bat. Level 19 is 6,859 and level 20 is 8,000! That’s 1141 gap, quite a bit bigger!
You simply change the exponent to see how the growth will be. This gives you a small increase in the beginning in comparison to the giant growth at the end. Very handy for large numbers in things like monster HP or Gold given.
Having trouble with the numbers because 2 is too small and 3 is too big? Don’t use whole numbers! 2.5 is just as valid as 2 or 3.
Keep in mind that the entire purpose of this is to be able to plan ahead and see the future. If I look at a monster level of 20 and see they will have 1000 HP, I know by the time the player runs into them they will need to deal with 1000 HP monsters.
You might think that using an exponential function is sloppy, and that’s because it kind of is. You don’t always want an increase, that’s boring. You want peaks and valleys! You could do all sorts of tweaking, like changing your “X” variable halfway through, but that’s a lot of effort. Instead you can also use a polynomial function for the same thing! Wouldn’t you know it, there’s a Polynomial worksheet in the Excel document already made up for you to open up.
Here’s our formula: ?x^? + ?x – ?
Let’s use this for Monster HP again. That’s our end result.
We want to change it via level, so that’ll be X (column F).
But now we have these four arbitrary numbers left! What do we do with those?
We fill them in!
The second number causes the biggest change (column C). It is the “exponential” part of all this. I’d suggest adding that in first. Since it’s exponential, I’d suggest starting small, like 1.2.
The first number (column B) helps modify the second number (column C). The bigger column C’s number is, the more drastic the change. If you kind of like what that gives you and want to modify it a tiny bit, edit the first arbitrary number in column B.
The third arbitrary number is a “direct multiplier” (column D). In the formula it’s simply “Level * Number”. So if you make it “5”, at level 2 you’ll get plus 10. This is a pretty minor change overall, but allows you to manipulate things by a bit to your liking. Remember that you can use a RANDBETWEEN function in Excel to keep it from getting stale and create those peaks and valleys we want.
The fourth is the “minor change” (column E); you simply subtract it from the total. You can use this as kind of dampening agent on the formula.
The third and fourth are useful for randomization! Again, the higher distance between the numbers the more variance you’ll have. You can make these ‘non significant numbers’ incredibly significant. I went ahead and made them RANDBETWEEN functions in the excel document for you.
Logarithmic Function
So you’ve mastered Linear Functions for when you want something to increase forever at a constant rate and you’ve got exponential and polynomial equations down when you want things to increase with a bit more spice.
What about when you want things to increase faster early on, but kind of “cap out” earlier on and not increase as much? A good example for something like this would be a stat like Luck or Evasion – you can’t let those get TOO high or they become ridiculous, and they’re often supplemented mostly by equipment or abilities rather than your level.
Logarithmic functions to the rescue! There’s a lot of different ways we can make these, but I’m focused on simplicity. What we’re going to do is Log of x divided by Log of y. In Excel is would look like LOG(X)/LOG(Y). It’s already set up in the Logarithmic Function worksheet in the Excel document for you.
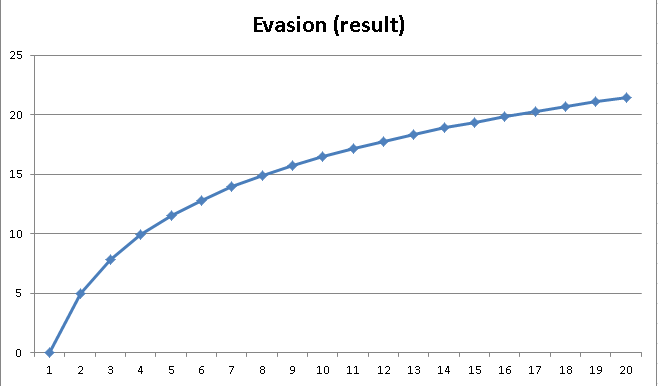
For us, X would be the level (column D). This number will be divided by another number, the LOG of Y (column C). When you mess with Y in excel, you’ll notice something weird – that the higher Y gets, the LOWER your result gets! You’ll also find that Y needs to be over 1. For your purposes, you’ll likely find your results to be best somewhere between 1 and 2.
The stat we’re looking for is Evasion, so we’ll want our result to be decently low. Let’s set our arbitrary value at “1.5” to start. So now we’ll see our Evasion move to 1 at level 2, then 2 at level 3, then 3 for level 4 and 5, etc., etc. You’ll see that as time goes on the difference between the two stats get less and less.
Now you may not like these results. You want things to start off big but then taper off, but you want the results to be bigger.
The precise way is to change your “Y” variable. We set ours at 1.5 and want a larger result, so we LOWER it closer to 1 (but ABOVE one). You COULD just fiddle with the numbers until something “looks” right, but that’d take forever if you don’t know what you’re looking for. An easier and better strategy is to figure out what you WANT the result to be and putting that in.
Let’s say I want my MAXIMUM natural evasion at level 100 to be around 30, give or take a bit, and I want my player to start getting serious diminishing returns around level 10. By fiddling with the arbitrary value I can land on 1.15 and I can get pretty close to what I want. ~15% evasion at level 10 and ~33% evasion at level 100. I’ve accomplished my goal of implementing evasion but limiting it.
You can manipulate the base logarithmic function pretty easily to make it what you want, even if you don’t understand how it works. This will help you have an appropriate and balanced curve that fits your desires.
Sigmoid Curve
The last one! Also one of the most useful and one I used for Spiff Spacely!
The logarithmic function is pretty helpful at making something grow fast early on and then kind of taper off, but figuring out exactly what to put in can be pretty annoying. Lots of trial and error. Wouldn’t it be easier if you could just say “This is my maximum value” and go from there? That’d be super helpful, especially for things like HP!
Enter the Sigmoid Curve! Open the “Logistic Function” worksheet in the Excel document.
You’ll be using the formula “=A2/(1+B2*EXP(C2*D2))” in Excel. Looks pretty complicated! If you’re unfamiliar with excel, get familiar! The bolded parts are referring to cell locations.
Columns A, B, and C are each going to have constant in them – they won’t change at all once you put them in there.
In the “A” field, you’ll be putting your maximum value. So if you’re making an RPG and you want your HP to cap out at 9,999, you’d put 9999 for everything in the A column. If you were messing with evasion and wanted natural evasion to cap out at 35%, you’d put 35 in cell A2.
The B and C fields are your limiters. The LOWER that B and C are, the earlier you will “cap out”. This will take some fiddling. For now, let’s put the B column at “50”. The C column needs to be negative and below 1 to get what we want. For now, put in -.08 in cell C2.
Column “D” is the thing that changes. In our example case, that’s our player’s level.
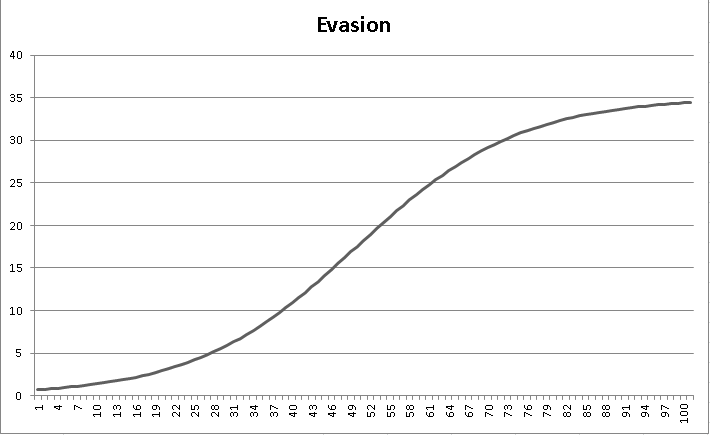
If you make a chart in excel it’ll look like this:
It gives kind of an “S” shaped curve, where it caps out around whatever you put in the “A” column; in our case, 35.
If you fiddle with the numbers, you’ll notice that you can make BIG changes occur by lowering C2. You’ll also notice that the EARLYnumbers are changed way more by B2.
It’ll take some fiddling, but experiment some with the curve. If you like the early part and want to make some tweaks to the later part, tweak C. If you like the later part and want to make some tweaks to the early part, tweak B. With some experimentation you can find a good middle ground between the two.
Final Thoughts
That was a long read. I hope you find the Excel workbook useful for your own purposes! Planning ahead is the biggest time saver a game designer can have. You don’t want to get halfway through your game and realize everything is falling apart! It’s worth the effort to plan ahead.
To recap:
Linear Equations are for constant growth
Exponential Functions are for exponential growth
Polynomial Functions are a more controllable alternative to exponential functions
Logarithmic Functions are for when you want stats to increase at a slower rate the higher you get
Logistic Functions are for when you have an end goal in mind and want to control the path to get there.